Systèmes linéaires

Sommaire

Ce document ne saurait remplacer un cours car il ne comporte aucune démonstration. Il peut permettre de revenir sur la théorie des systèmes linéaires avec recul sans être uniquement occupé par les calculs. Réfléchir aux données avant de calculer et aux résultats après avoir calculé doit permettre de calculer plus intelligemment et d'interpréter avec pertinence les solutions.

Pour les étudiants préparant le CAPES, il propose de voir les systèmes linéaires comme une approche essentielle des sous-espaces affines : l'ensemble des solutions d'un système linéaire, s'il n'est pas vide, est un sous-espace affine de direction le sous-espace vectoriel des solutions du système homogène associé. Une solution particulière est un point de ce sous-espace affine.

Définitions et propriétés
Résolution des systèmes linéaires échelonnés
Méthode de Gauss
Utilisation des déterminants (Cette partie est destinée aux étudiants de second cycle.)

Ce document mis en ligne par Marie-Claude David a pour base essentielle le résumé de cours du S2 MIAS rédigé par Myriam Déchamps. Les remarques sur les algorithmes sont dues à Karim Belabas.

Définitions et propriétés

Système linéaire

Soient

p \geq 1

n \geq 1

deux nombres entiers. On appelle système linéaire de $p$ équations (scalaires) à $n$ inconnues à coefficients dans un corps $K$ un ensemble d'équations de la forme

(S)

(S) {\begin{array}{rcrcrcl} a_{1, 1} x_{1} & + & \dots & + & a_{1, n} x_{n} & = & b_{1} \\ a_{2, 1} x_{1} & + & \dots & + & a_{2, n} x_{n} & = & b_{2} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ a_{p, 1} x_{1} & + & \dots & + & a_{p, n} x_{n} & = & b_{p} \end{array}

où :

les $a_{i, j}, 1 \leq i \leq p, 1 \leq j \leq n$ sont des scalaires dans $K$ , appelés les coefficients du système ;
les vecteurs $u_{j} = (a_{1, j}, a_{2, j}, \dots, a_{p, j})$ de $K^{p}, 1 \leq j \leq n$ sont les vecteurs colonnes du système ;
les $b_{i}, 1 \leq i \leq p$ , sont des scalaires dans $K$ , appelés les seconds membres du système ; le n-uplet $b = (b_{1}, \dots, b_{p})$ de $K^{p}$ est le second membre du système ;
les $x_{i}, 1 \leq i \leq n$ sont les inconnues , que l'on cherche dans $K$ ; $(x_{1}, \dots, x_{n}) \in K^{n}$ est le n-uplet inconnu ;
la matrice $p \times n$ à coefficients dans K :
$A = (\begin{array}{cccc} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ a_{p, 1} & a_{p, 2} & \dots & a_{p, n} \end{array})$
est appelée la matrice du système linéaire $(S)$ . Soit $B = (b_{i})_{1 \leq i \leq p}$ le vecteur colonne second membre de $(S)$ . L'écriture matricielle du système est $A X = B$ , c'est-à-dire :
$(\begin{array}{cccc} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ a_{p, 1} & a_{p, 2} & \dots & a_{p, n} \end{array}) (\begin{array}{c} x_{1} \\ ⋮ \\ x_{n} \end{array}) = (\begin{array}{c} b_{1} \\ ⋮ \\ b_{p} \end{array})$

Solution et compatibilité

Un $n$ -uplet $(x_{1}, \dots, x_{n}) \in K^{n}$ est une solution de $(S)$ si elle vérifie les $p$ équations du système ;
Résoudre $(S)$ c'est décrire l'ensemble $𝒮$ des solutions de $(S)$ ;
Le système $(S)$ est compatible s'il admet au moins une solution ; sinon, $(S)$ est dit incompatible ;
On dit que $S$ est un système homogène si le second membre $b$ est nul ;
Le système linéaire obtenu lorsqu'on remplace dans $(S)$ le n-uplet $b$ par le n-uplet $(0, \dots, 0)$ s'appelle le système homogène associé à $(S)$ .

Propriétés

Un système homogène est toujours compatible puisqu'il admet le n-uplet $(0, \dots, 0)$ comme solution.
L'ensemble des solutions d'un système homogène est un sous-espace vectoriel.
Si $s_{1}$ et $s_{2}$ sont des solutions d'un système linéaire $(S)$ , $s_{1} - s_{2}$ est une solution du système homogène associé $(S_{0})$ .
Si $s$ est une solution d'un système linéaire $(S)$ , alors on obtient toutes les solutions de $(S)$ en ajoutant à $s$ les solutions du système homogène associé $(S_{0})$ , c'est-à-dire :
$𝒮 = s + 𝒮_{0} .$
L'ensemble des solutions de $(S)$ est donc le sous-espace affine de $ℝ^{n}$ passant par $s$ et de direction $𝒮_{0}$ .

On peut considérer chaque équation du système comme l'équation d'un hyperplan affine, l'ensemble des solutions du système est alors l'intersection des

p

hyperplans affines. La question de la compatiblité d'un système linéaire est donc fondamentale. Un système homogène est toujours compatible, en effet une intersection de sous-espaces vectoriels n'est jamais vide. Si le système n'est pas homogène, il représente une intersection de sous-espaces affines qui peut être vide dans le cas d'un système incompatible.

Exercices

Exercices simples de modélisation

Résolution des systèmes linéaires échelonnés

Matrice échelonnée

Une matrice

A = (a_{i, j})_{1 \leq i \leq p, 1 \leq j \leq n} \in M_{p, n} (K)

est dite échelonnée ou en échelons s'il existe un entier

r

1 \leq r \leq \min (p, n)

et une suite d'entiers

1 \leq j_{1} < j_{2} < \dots < j_{r} \leq n

tels que :

$a_{i, j_{i}} \neq 0, 1 \leq i \leq r, a_{i, j} = 0, 1 \leq i \leq r, 1 \leq j < j_{i}$ ( $i \geq 2$ si $j_{1} = 1$ ) ; (c'est-à-dire que les $a_{i, j_{i}}$ sont les premiers coefficients non nuls des $r$ premières lignes, on les appelle pivots et on remarque qu'il n'y a qu'un pivot par ligne et par colonne.)
$a_{i, j} = 0, r < i \leq p, 1 \leq j \leq n .$ (c'est-à-dire que toutes les lignes après les $r$ premières sont nulles)

Exemple.

Considérons les matrices de

M_{4, n} (K)

$A = (\begin{matrix} 2 & a_{1, 2} & a_{1, 3} & \dots & \dots & a_{1, n} \\ 0 & 0 & 5 & a_{2, 3} & \dots & a_{2, n} \\ 0 & 0 & 0 & 7 & \dots & a_{3, n} \\ 0 & 0 & 0 & 0 & \dots & 0 \end{matrix}) B = (\begin{matrix} 1 & a_{1, 2} & a_{1, 3} & \dots & \dots & a_{1, n} \\ 0 & 0 & 0 & 0 & \dots & 0 \\ 0 & 0 & 0 & \dots & 0 & 3 \\ 0 & 2 & 0 & 0 & \dots & 0 \end{matrix})$

La matrice

A

est échelonnée, la matrice

B

ne l'est pas.
Voici un autre exemple de matrice échelonnnée que vous pouvez :

Exercice. Cette matrice est-elle échelonnée ?

Système linéaire échelonné

Un système linéaire A X=B possédant une matrice échelonnée est dit échelonné ; l'entier r s'appelle le rang du système (ou de la matrice A du système), les inconnues sont les inconnues principales et les autres inconnues sont dites non principales ou secondaires . Enfin, les coefficients non nuls , sont les pivots du système.

Compatibilité

cas r=p Le système linéaire est compatible. L'égalité r=p signifie que les conditions imposées aux variables (les équations) sont indépendantes donc compatibles entre elles.
cas r<p Les p-r dernières équations ont leurs premiers membres nuls, donc le système est compatible si et seulement si les p-r derniers seconds membres sont nuls. On a donc p-r conditions de compatibilité à vérifier.

Exercice. Questions sur le rang et la compatibilité

Résolution

Si le système n'est pas compatible, par définition son ensemble de solutions est vide. S'il est compatible, on fait passer les inconnues secondaires dans le second membre et on les considère comme des paramètres (on a donc n-r paramètres) et on résout le système en commençant par calculer x_r dans la dernière équation et en remontant.

Bien sûr si on a l'égalité n=r, alors la solution, quand elle existe , est unique. Dans le cas particulier : r=p=n, le système est dit de Cramer, il a une et une solution.

Exercice. Inconnues principales, secondaires

En résumé, l'ensemble des solutions peut être vide (système incompatible), contenir un unique élément (système compatible et r=n) ou une infinité.

Conseils pour la résolution d'un système linéaire échelonné

On commence par déterminer r, p et n puis on dresse la liste des cas possibles :

système incompatible
système compatible et solution unique. Indiquez le nombre de conditions de compatibilité.
système compatible et infinité de solutions. Indiquez le nombre de conditions de compatibilité et le nombre de paramètres.

Avant de se lancer dans des calculs, il est important d'avoir une idée sur le type possible de l'ensemble des solutions.

A la fin des calculs, on présente l'ensemble des solutions sous la forme de la somme d'une solution particulière et de l'ensemble des solutions du système homogène (présentées comme combinaison linéaire de n-r solutions indépendantes).

Exemple 1. On résoud le système linéaire :

Première étape
: C'est un système de Cramer. Une et une seule solution.
Deuxième étape
Il se résoud à partir de x₃, on obtient
x₃=2 puis et enfin
L'ensemble de solutions est .
Exemple 2. On résoud le système linéaire :

Première étape
r=p=3 et n=4 : Le système est compatible. Les solutions dépendent d'un paramètre.
Deuxième étape
On passe x₄ au second membre comme un paramètre :

puis, on résoud à partir de x₃, on obtient :
puis et enfin
L'ensemble des solutions est
Exemple 3. On résoud le système linéaire :

Première étape
r=3 et p=4 : Il y a une condition de compatibilité à vérifier.
r=n : La solution si elle existe est unique.

Deuxième étape
Le système n'est compatible que dans le cas et on obtient alors la solution unique (x₁,x₂,x₃)=(-1,1,2).

La conclusion s'écrit :
- Cas :
- Cas :
Exemple 4. On résoud le système linéaire :
Première étape
r=3 et p=4 : Il y a une condition de compatibilité.
r=3 et n=4 : Quand il est compatible, le système a une infinité de solutions dépendant d'un paramètre.

Deuxième étape
- Cas :
- Cas :

A vous de travailler : Résolution d'un système échelonné

Parfois, on peut trouver l'ensemble des solutions sans résoudre le système.

Exercice 1
Exercice 2

Méthode de Gauss

La méthode de Gauss permet d'obtenir un système linéaire échelonné (donc qu'on sait résoudre) équivalent à un système donné.

Définitions

Deux systèmes linéaires sont équivalents s'ils ont le même ensemble de solutions.

Dans toute la suite, (S) est un système linéaire de p équations, n inconnues, à coefficients dans K.

On appelle tableau complet du système linéaire (S) le tableau de nombres suivant :

(à la gauche de la barre il y a les coefficients de la matrice du système, à la droite la matrice colonne du second membre)

On appelle opération élémentaire sur (S) (ou sur les lignes de son tableau complet) une des opérations suivantes :

Permuter deux lignes.
Multiplier une ligne par un scalaire non nul .
Ajouter à une ligne une combinaison linéaire des autres lignes, c'est-à-dire une somme de multiples scalaires des autres lignes.

Proposition

Toute opération élémentaire sur un systéme linéaire (S) le transforme en un système linéaire équivalent.
Il existe une suite finie d'opérations élémentaires qui transforme le système linéaire (S) en un système échelonné.

La méthode du pivot de Gauss de résolution d'un système linéaire (S) consiste à :

écrire le tableau complet du système ;
effectuer sur ce tableau des opérations élémentaires dans un ordre bien déterminé de façon à transformer la matrice A du système en une matrice échelonnée A' ;
résoudre le système échelonné (S') correspondant, équivalent à (S) : l'ensemble des solutions de (S') est l'ensemble des solutions de (S).

Remarques

Pour alléger l'écriture, on effectue les opérations élémentaires sur le tableau des coefficients. Il faut garder à l'esprit que ces tableaux représentent des systèmes équivalents.
Il y a en général plusieurs choix d'opérations élémentaires qui permettent de transformer un système linéaire en système échelonné équivalent. Ces différents choix peuvent conduire à écrire la solution générale du système sous des formes différentes (inconnues principales ou solutions particulières différentes). Pour faciliter la comparaison des solutions et la vérification, il est conseillé d'écrire les solutions comme somme d'une solution particulière de (S') et d'une combinaison linéaire de solutions particulières de (S'₀) (les coefficients étant les inconnues secondaires). Ainsi pour vérifier le résultat, il suffit d'injecter la particulière de (S') et celles de (S'₀) dans les systèmes (S) et (S₀).
Notre description de la méthode de Gauss suppose que le système est connue de façon exacte. C'est rarement le cas dans les applications pratiques où seules des quantités approchées sont disponibles, par exemple fournies par des mesures physiques. Que signifie une solution exacte d'un système approché ? Il n'est en rien évident (c'est en général faux) que ce soit une solution approchée du système exact.

Exercices

Voici pour commencer un exercice traité : Exemple.

Résoudre dans le système :

Solution : Le tableau du système se transforme ainsi par les opérations élémentaires indiquées (tous les systèmes représentés par les tableaux suivants sont équivalents):

Le système est de rang 2, il est compatible puisqu'il est équivalent à un système dont le rang est égal au nombre d'équations. Les inconnues principales sont x et z. Les inconnues secondaires y et t sont des paramètres alpha

.
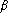On trouve facilement une solution particulière de (S') en annulant alpha

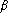: . On vérifie que s est solution de (S).
La solution générale de (S'₀) est

On vérifie que et sont solutions de (S₀).

La conclusion s'écrit : L'ensemble des solutions de (S) est :

puis deux exercices WIMS :

Mise en oeuvre de la méthode de Gauss : Les exercices de "Gauss visuel" proposent de résoudre des systèmes linéaires par la méthode de Gauss. L'étudiant choisit les opérations élémentaires à effectuer et la machine les fait pour lui.
Analyse des solutions d'un système linéaire à paramètre : Il s'agit de répondre à des questions sur l'ensemble des solutions d'un système après l'avoir échelonné.

Utilisation des déterminants

La méthode de Gauss est la plus efficace en particulier pour la programmation mais l'utilisation des déterminants peut avoir son intérêt pour les petits systèmes ou les questions théoriques.

D'un point de vue algorithmique, la méthode de Gauss est plus générale puisque elle permet de résoudre les systèmes non carrés ou singuliers. Elle est aussi plus rapide dès que les déterminants ne se calculent pas de tête : elle résoud un système linéaire n x n en Cn³ opérations dans le corps K (additions, multiplications, divisions), pour une petite constante C. Celle de Cramer requiert le calcul de n + 1 déterminants, qu'un algorithme naïf calculera à l'aide de la ... méthode de Gauss, en Cn⁴ opérations donc. Par exemple pour n=50, un ordinateur qui effectue un milliard d'opérations par seconde mettra environ années pour faire le calcul avec la méthode de Cramer et seconde avec une méthode mieux adaptée. (D'après Algèbre linéaire numérique de G. Allaire et S.M.Kaber Ellipses)

Rang

Le rang r du système est aussi l'ordre des plus grands déterminants non nuls extraits de sa matrice.

On garde les notations précédentes ; quitte à changer l'ordre des équations et des inconnues, on peut supposer que le déterminant n'est pas nul. En termes de vecteurs colonnes, ceci signifie que les les vecteurs u₁, u₂, ldots , u_r sont linéairement indépendants alors que pour j = r+1,..., n, u_j est combinaison linéaire des vecteurs u₁, u₂, ... , u_r.

Compatibilité

Le système est compatible si et seulement si le vecteur second membre b est combinaison linéaire des u₁, u₂,..., u_n. Les coefficients d'une telle combinaison forment une solution du système.

On peut traduire cette condition de plusieurs façons équivalentes :

La matrice a le même rang que A. (La matrice est la matrice à p lignes et n+1 colonnes obtenue en accollant la colonne second membre à la matrice A .)
Le vecteur b est combinaison linéaire des u₁, u₂, ... , u_r.
Pour i = r+1, ..., p, le déterminant bordant de D est nul :

Le déterminant est obtenu en bordant D avec la colonne du second membre et la i-ème ligne. Il y a p-r déterminants bordants, on retrouve les p-r conditions de compatibilité.

exercice

Formules de Cramer

On peut exprimer les solutions d'un système de Cramer à l'aide des formules de Cramer :

On note D le déterminant de la matrice du système (on rappelle qu'un système de Cramer est carré) et D_j le déterminant calculé en remplaçant dans D la j-ème colonne par le second membre :

L'unique solution du sytème est où s_j vaut .

Ces formules peuvent être efficaces pour conserver les symétries d'un système linéaire.
Exemple

Soient a, b, c, et des réels tels que a, b et c ne soient pas nuls ensemble. Résoudre le système . (On traitera un seul cas pour chaque valeur du rang de .)

Solution Le déterminant de ce système est un déterminant de Vandermonde qui vaut D=(c-a)(c-b)(b-a).

Cas a, b et c distincts : Si D n'est pas nul, c'est-à-dire si les paramètres a, b et c sont distincts alors le système a une unique solution donnée par les formules de Cramer par exemple.

Les expressions sont semblables par permutation circulaire.
Cas a 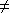b et b=c : Le système est de rang 2 et il est compatible si et seulement si le bordant D_z est nul c'est-à-dire si et seulement si 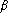vaut .
Si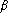 est différent de , le système n'a pas de solution.
Sinon les solutions du système forment une droite affine D qui a pour équations x+y+z=1 et . Un point particulier de cette droite est et le vecteur (0, 1, -1) est l'un de ses vecteurs directeurs.
Cas a=b=c : Le système est de rang 1 et il est compatible si et seulement si et .
Si et , l'ensemble des solutions est le plan affine d'équation x+y+z=1.
Sinon, il est vide.

Les autres cas se traitent de même puisque les trois paramètres jouent des rôles symétriques.

Remarque : Ces formules peuvent être utilisées pour résoudre n'importe quel système compatible, par exemple pour calculer une solution particulière. En effet on a vu que tout système linéaire compatible peut être considéré comme un système de Cramer pour peu qu'on passe les inconnues secondaires dans le second membre et qu'on les considère comme des paramètres. Une solution particulière est obtenue en annulant tous ces paramètres.

document sur les définitions et méthodes de résolution des systèmes linéaires.
: linear_system, gauss_algorithm, determinant, interactive mathematics, interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.