Géométrie du plan complexe
Géométrie du plan complexe
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Voici un cours sur la géométrie du plan complexe avec des figures et des exercices interactifs. Avant de l'aborder, il serait bon de maîtriser le contenu et les exercices du cours Nombres complexes . Pour l'étude des isométries, il est utile de se référer au document Isométries du plan .
Version pdf de ce cours avec liens vers les exercices.
Avertissement
Ce cours est une partie de l'option de géométrie enseignée de 2013 à 2015 au premier semestre de la première année de licence MPI à la Faculté des Sciences d'Orsay de l'université Paris Sud. Il s'agissait de pallier l'absence des transformations au Lycée.
Pour afficher les figures mobiles GeoGebra, il faut activer WebGL sur son navigateur.
II Ecriture complexe d'une transformation
III Isométries du plan complexe
VI Etude des similitudes qui ne sont pas des isométries
I Géométrie du plan complexe
Géométrie du plan complexe
→ I Géométrie du plan complexe
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Dans cette partie, on complète les propriétés géométriques des affixes vues dans le document
Nombres complexes
.
Géométrie du plan complexe
→ I Géométrie du plan complexe
I-1 Affixe d'un vecteur, angle orienté de deux vecteurs
Géométrie du plan complexe
→
I Géométrie du plan complexe
→ I-1 Affixe d'un vecteur, angle orienté de deux vecteurs
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Définition
Dans le plan orienté par un repère orthonormé
, on considère un vecteur
de composantes
; on appelle affixe du vecteur
le nombre complexe
.
En particulier, l'affixe de
est égal à celui de
. L'affixe du vecteur
est
quand
et
sont des points d'affixes respectives
et
.Proposition
Soient
et
deux vecteurs non nuls d'affixes respectives
et
. L'angle orienté
a pour mesure l'argument de
.
Pour et deux points distincts d'affixes respectives et et et deux points distincts d'affixes respectives et , l'angle orienté a pour mesure l'argument de .
Pour et deux points distincts d'affixes respectives et et et deux points distincts d'affixes respectives et , l'angle orienté a pour mesure l'argument de .
Démonstration
Par relation de Chasles, on a
La formule est démontrée et s'applique à
pour donner :
Fin de la démonstration
Exercice
Angle et quotient de complexes
Géométrie du plan complexe
→
I Géométrie du plan complexe
→ I-1 Affixe d'un vecteur, angle orienté de deux vecteurs
I-2 Applications à l'étude de lieux
Géométrie du plan complexe
→
I Géométrie du plan complexe
→ I-2 Applications à l'étude de lieux
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Ces descriptions sont des applications directes des propriétés du module et de l'argument d'un nombre complexes.
Soient , et des points d'affixes respectives , et .
Soient , et des points d'affixes respectives , et .
- L'ensemble des points vérifiant est la médiatrice de , ensemble des points équidistants de et .
- L'ensemble des points vérifiant est le cercle centré en passant par .
- L'ensemble des points vérifiant est le disque unité ouvert (c'est-à-dire le disque sans le cercle unité).
- L'ensemble des points vérifiant est le disque unité fermé (c'est-à-dire avec le cercle unité).
- L'ensemble des points vérifiant ne contient pas donc on peut poser ; la condition s'écrit alors . L'ensemble des points vérifiant est la droite .
- L'ensemble des points vérifiant ne contient pas donc on peut poser ; la condition s'écrit alors . L'ensemble des points vérifiant est la droite .
- Les points tel que soit égal à sont les intersections du cercle de diamètre et de la médiatrice de en effet le triangle est rectangle isocèle en .
- Les points
tel que
soit un imaginaire pur sont les points différents de
du cercle de diamètre
en effet le triangle
est rectangle en
.
Exercices
Déterminer le troisième sommet d'un triangle.
- Triangle isocèle (1)
- Triangle isocèle (2)
- Triangle équilatéral
Géométrie du plan complexe
→
I Géométrie du plan complexe
→ I-2 Applications à l'étude de lieux
II Ecriture complexe d'une transformation
Géométrie du plan complexe
→ II Ecriture complexe d'une transformation
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Un point dans le plan avec un repère orthonormé
peut être déterminé par ses coordonnées
ou son affixe
. Ainsi on peut définir une transformation en donnant pour chaque point les coordonnées de son image ou son affixe.
Définition
Soient deux nombres complexes
(non nul) et
. On s'intéresse aux transformations
et
définies pour
par :
Géométrie du plan complexe
→ II Ecriture complexe d'une transformation
II-1 Exemples
Géométrie du plan complexe
→
II Ecriture complexe d'une transformation
→ II-1 Exemples
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Les transformations présentées ici sont définies dans le document
Isométries du plan
sauf l'homothétie (voir
ici
).
On considère et d'affixes respectifs et .
Image par une rotation
On considère et d'affixes respectifs et .
- La transformation est la translation de vecteur d'affixe b. En effet, de , on tire : puisque est l'affixe de .
- La transformation est la symétrie centrale de centre d'affixe . en effet, de , on tire donc est le milieu de .
- Pour réel, non nul et différent de , et , est l'homothétie de centre d'affixe et de rapport . En effet, pour , on a : .
- Pour
, l'image de
par la rotation de centre
d'affixe
et d'angle
est le point
dont l'affixe vérifie :
- La transformation est la réflexion d'axe : .
- Pour et , est la réflexion d'axe où est la droite passant par et tel que . En effet, de , on tire : .
Exercice
Image par une rotation
Géométrie du plan complexe
→
II Ecriture complexe d'une transformation
→ II-1 Exemples
II-2 Propriétés générales
Géométrie du plan complexe
→
II Ecriture complexe d'une transformation
→ II-2 Propriétés générales
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Soient
et
deux nombres complexes.
Les applications et multiplient les longueurs par .
Les applications conservent les angles orientés.
Les applications transforment un angle orienté en son opposé.
Les applications et multiplient les longueurs par .
Les applications conservent les angles orientés.
Les applications transforment un angle orienté en son opposé.
Démonstration
Soient
et
d'affixes respectives
et
; on note
et
les affixes de leurs images.
Pour les applications , on a : d'où .
Pour les applications , on a : d'où .
Dans les deux cas, la longueur est le produit de par .
On suppose et distincts et on considère deux autres points distincts et d'affixes respectives et ; on note et les affixes de leurs images.
Pour les applications , on a : donc les angles orientés sont conservés.
Pour les applications , on a : donc un angle orienté est transformé en son opposé.
Pour les applications , on a : d'où .
Pour les applications , on a : d'où .
Dans les deux cas, la longueur est le produit de par .
On suppose et distincts et on considère deux autres points distincts et d'affixes respectives et ; on note et les affixes de leurs images.
Pour les applications , on a : donc les angles orientés sont conservés.
Pour les applications , on a : donc un angle orienté est transformé en son opposé.
Fin de la démonstration
Géométrie du plan complexe
→
II Ecriture complexe d'une transformation
→ II-2 Propriétés générales
III Isométries du plan complexe
Géométrie du plan complexe
→ III Isométries du plan complexe
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
On suppose dans cette partie que
est de module
.
D'après la proposition , les applications étudiées sont donc des isométries.
D'après la proposition , les applications étudiées sont donc des isométries.
Géométrie du plan complexe
→ III Isométries du plan complexe
III-1 Isométries positives
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-1 Isométries positives
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-1 Isométries positives
III-1-1 Etude de
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-1 Isométries positives
→ III-1-1 Etude de
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Pour
, l'application
est une isométrie positive.
- Pour et , est l'identité.
- Pour , est la translation de vecteur d'affixe b.
- Pour , on pose avec . Alors est la rotation de centre d'affixe et d'angle .
Démonstration
Pour l'essentiel, ces résultats ont été vus dans les exemples
ici
.
L'équation aux points fixes donne la valeur de . Si on soustrait cette relation à , on obtient , donc est la rotation de centre et d'angle .
L'équation aux points fixes donne la valeur de . Si on soustrait cette relation à , on obtient , donc est la rotation de centre et d'angle .
Fin de la démonstration
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-1 Isométries positives
→ III-1-1 Etude de
III-1-2 Exemple
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-1 Isométries positives
→ III-1-2 Exemple
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soit
l'application du plan complexe définie par :
Comme
est de la forme
avec
de module
,
est une isométrie positive qui n'est pas une translation donc c'est une rotation.
Son centre est le point d'affixe vérifiant l'équation au point fixe :
donc
a pour affixe
.
L'angle de est l'argument de soit .
Pour conclure, est la rotation où le point d'affixe .
Son centre est le point d'affixe vérifiant l'équation au point fixe :
L'angle de est l'argument de soit .
Pour conclure, est la rotation où le point d'affixe .
Remarque
Pour résoudre l'équation au point fixe, il est recommandé de savoir calculer un quotient de nombres complexes. On trouvera la méthode à cette page
Quotient de nombres complexes
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-1 Isométries positives
→ III-1-2 Exemple
III-2 Isométries négatives
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-2 Isométries négatives
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-2 Isométries négatives
III-2-1 Etude de
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-2 Isométries négatives
→ III-2-1 Etude de
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Pour
, l'application
est une isométrie négative.
- Pour , l'application est une réflexion d'axe passant par le point d'affixe et faisant l'angle avec l'axe des abscisses. L'axe est aussi la médiatrice de où est le point d'affixe .
- Pour , l'application est une symétrie glissée composée de la translation de vecteur d'affixe et de la réflexion avec . Son axe est la droite passant par d'affixe et dirigée par . Il fait un angle de avec l'axe des abscisses.
Démonstration
Dans cette démonstration, on utilise de manière essentielle, la classification des isométries (
Isométries du plan
).
L'isométrie est négative donc est une réflexion ou une symétrie glissée.
Considérons le point d'affixe , image de par et le milieu (d'affixe ) de . Le point appartient donc à l'axe de . Alors est une réflexion si et seulement si est fixe par .
Donc
est fixe par
si et seulement si
.
L'isométrie est négative donc est une réflexion ou une symétrie glissée.
Considérons le point d'affixe , image de par et le milieu (d'affixe ) de . Le point appartient donc à l'axe de . Alors est une réflexion si et seulement si est fixe par .
- Pour
, l'isométrie
est une réflexion d'axe
passant par
.
Si vaut , l'isométrie est une réflexion d'axe parallèle à l'axe des abscisses. En effet, est la translation de vecteur donc les axes de et sont parallèles.
Si est différent de , est la composée donc la rotation (qui est une rotation d'angle ) est la composée . Donc l'axe de fait un angle avec l'axe des abscisses, axe de .
Pour toute valeur de , on a donc .
On peut aussi remarquer que, comme est la réflexion qui échange et , son axe est la médiatrice de . - Pour
, calculons
pour
, image de
par
.
Sur son axe, la symétrie glissée agit comme la translation de vecteur . L'isométrie est donc la symétrie glissée composée de la translation de vecteur et de la réflexion avec .
En effet, on a :De plus vérifie : . Donc est bien une réflexion et bien sûr, son axe passe par et est dirigé par .
On peut remarquer que, l'axe de étant par définition celui de , il fait donc un angle de avec l'axe des abscisses.
Fin de la démonstration
Remarque
L'expression complexe de
est
. On constate que
est une involution (donc une réflexion) si et seulement si
est nul. Sinon
est la translation de vecteur
. Ceci est cohérent avec l'étude précédente.
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-2 Isométries négatives
→ III-2-1 Etude de
III-2-2 Exemple
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-2 Isométries négatives
→ III-2-2 Exemple
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soit
l'application du plan complexe définie par
Comme
est de la forme
avec
de module
,
est un antidéplacement, c'est-à-dire une réflexion ou une symétrie glissée.
Dans les deux cas, le point
d'affixe
est un point de l'axe
de cet antidéplacement ; en effet
est le milieu de
.
Si est nul, le point est confondu avec qui est fixe et est une réflexion, son axe est la droite passant par et faisant un angle de avec l'axe des abscisses (voir ici ).
Si n'est pas nul, posons et notons le point d'affixe . Soit . Le point est fixe si et seulement si on a . Or on a :
Dans le cas où
n'est pas nul,
est fixe si et seulement si
vérifie
c'est-à-dire
.
Soit la droite passant par et faisant un angle de avec l'axe des abscisses. On a donc montré que est fixe si et seulement si appartient à la droite . On remarque que, dans ce cas, appartient aussi à .
En résumé si appartient à , admet un point fixe , c'est la réflexion d'axe passant par et faisant un angle de avec l'axe des abscisses. Evidemment est la médiatrice de et donc perpendiculaire à .
Quand n'appartient pas à , n'est pas fixe et n'a alors aucun point fixe, c'est une symétrie glissée d'axe passant par
et faisant un angle de
avec l'axe des abscisses. Le vecteur de la translation est
, il dirige l'axe et son affixe est
. On peut écrire
Dans cette expression, on voit clairement que l'argument de
est
passant par
et faisant un angle de
avec l'axe des abscisses. Le vecteur de la translation est
, il dirige l'axe et son affixe est
. On peut écrire
Dans cette expression, on voit clairement que l'argument de
est
Si est nul, le point est confondu avec qui est fixe et est une réflexion, son axe est la droite passant par et faisant un angle de avec l'axe des abscisses (voir ici ).
Si n'est pas nul, posons et notons le point d'affixe . Soit . Le point est fixe si et seulement si on a . Or on a :
Soit la droite passant par et faisant un angle de avec l'axe des abscisses. On a donc montré que est fixe si et seulement si appartient à la droite . On remarque que, dans ce cas, appartient aussi à .
En résumé si appartient à , admet un point fixe , c'est la réflexion d'axe passant par et faisant un angle de avec l'axe des abscisses. Evidemment est la médiatrice de et donc perpendiculaire à .
Quand n'appartient pas à , n'est pas fixe et n'a alors aucun point fixe, c'est une symétrie glissée d'axe
 passant par
et faisant un angle de
avec l'axe des abscisses. Le vecteur de la translation est
, il dirige l'axe et son affixe est
. On peut écrire
passant par
et faisant un angle de
avec l'axe des abscisses. Le vecteur de la translation est
, il dirige l'axe et son affixe est
. On peut écrire
Géométrie du plan complexe
→
III Isométries du plan complexe
→
III-2 Isométries négatives
→ III-2-2 Exemple
III-3 Exercices
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-3 Exercices
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
- Dans cet exercice, il s'agit de déterminer le type d'une isométrie donnée en écriture complexe et ses éléments caractéristiques.
Isométries en complexes - Dans celui-ci, on s'intéresse aux points fixes de la transformation.
Points fixes d'une isométrie
Géométrie du plan complexe
→
III Isométries du plan complexe
→ III-3 Exercices
IV Homothétie
Géométrie du plan complexe
→ IV Homothétie
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Nous commençons l'étude des transformations qui conservent les rapports des longueurs par celle de la plus simple d'entre elles, l'homothétie.
Géométrie du plan complexe
→ IV Homothétie
IV-1 Définition
Géométrie du plan complexe
→
IV Homothétie
→ IV-1 Définition
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
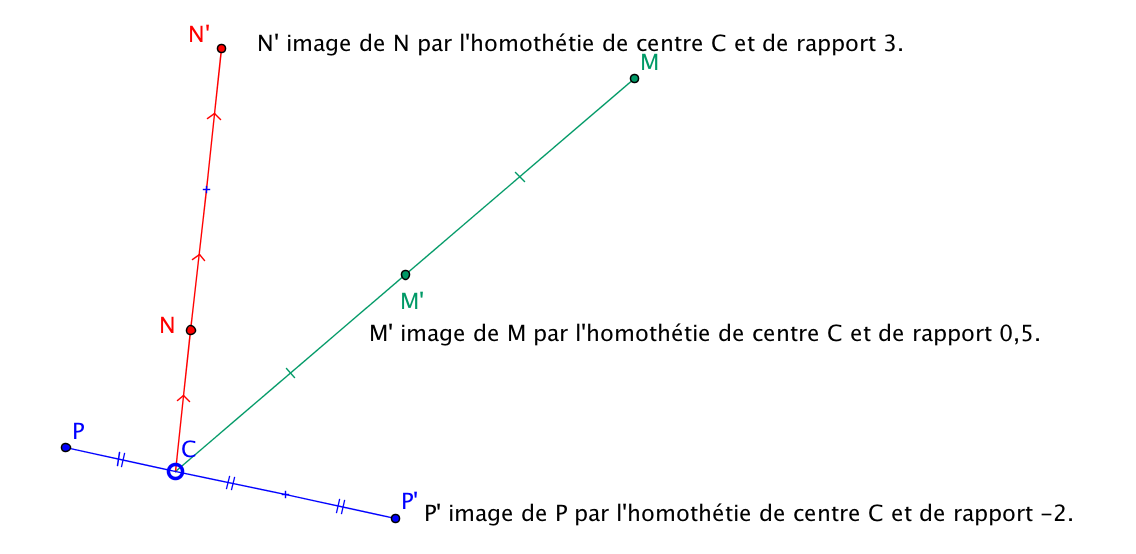
Définition
Soient
un point du plan
et
un réel non nul différent de
. On appelle homothétie de centre
et de rapport
, et on note
, l'application du plan affine
dans lui-même qui à un point
associe le point
tel que
.
Si est l'affixe de , l'écriture complexe de est .
Si est l'affixe de , l'écriture complexe de est .
Exemple
La symétrie centrale de centre
est l'homothétie de centre
de rapport
:
. On a déjà vu son expression complexe
ici
.
Géométrie du plan complexe
→
IV Homothétie
→ IV-1 Définition
IV-2 Figure mobile
Géométrie du plan complexe
→
IV Homothétie
→ IV-2 Figure mobile
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Sur la figure mobile (merci à Chantal Causse), l'image du F bleu par l'homothétie de centre I et de rapport k (qui peut varier grâce au curseur) est le F vert. Vous pouvez déplacer tous les objets rouges.
Géométrie du plan complexe
→
IV Homothétie
→ IV-2 Figure mobile
IV-3 Homothétique d'un pentagone
Géométrie du plan complexe
→
IV Homothétie
→ IV-3 Homothétique d'un pentagone
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Le polygone hachuré en vert est l'image du grand pentagone orange par l'homothétie de centre
et de rapport
donné par le curseur. On remarque qu'il est régulier et que ses côtés sont parallèles à ceux du grand.
Géométrie du plan complexe
→
IV Homothétie
→ IV-3 Homothétique d'un pentagone
IV-4 Propriétés
Géométrie du plan complexe
→
IV Homothétie
→ IV-4 Propriétés
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Soient
un réel non nul différent de
,
,
et
des points du plan.
Pour la démonstration de ces propriétés, on renvoie à celles des propriétés de la symétries centrale (voir
propriétés des symétries centrales
et
droites invariantes
dans le cours Isométries de plan.)- Une homothétie admet son centre comme unique point fixe.
- L'application multiplie les longueurs par . De ce fait, elle conserve les rapports de longueur.
- L'inverse de est .
- Une homothétie transforme une droite en une droite parallèle .
- Une homothétie conserve les milieux. Si est une homothétie, l'image par du milieu de est le milieu de .
- Les droites invariantes par sont celles passant par son centre .
Géométrie du plan complexe
→
IV Homothétie
→ IV-4 Propriétés
IV-5 Exercices
Géométrie du plan complexe
→
IV Homothétie
→ IV-5 Exercices
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
- Exercice de calcul
Image par homothétie ou translation
- Exercices graphiques
Image de points par une homothétie
Image d'un triangle par une homothétie (1)
Image d'un triangle par une homothétie (2)
Géométrie du plan complexe
→
IV Homothétie
→ IV-5 Exercices
V Similitudes
Géométrie du plan complexe
→ V Similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
On étudie maintenant les transformations
et
dans le cas où
n'est plus nécessairement de module
.
Géométrie du plan complexe
→ V Similitudes
V-1 Définitions et propriétés
Géométrie du plan complexe
→
V Similitudes
→ V-1 Définitions et propriétés
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Définition
Dans le plan muni d'un repère orthonormé direct,
on appelle similitude la composée d'une isométrie et d'une homothétie. La similitude est dite directe si l'isométrie est positive, indirecte si l'isométrie est négative.
Une similitude est donc de la forme si elle est directe ou si elle est indirecte.
Réciproquement, l'application (resp. ) est une similitude directe (resp. indirecte). En effet, quand on la compose par l'homothétie de centre et de rapport , on obtient une isométrie positive (resp. négative).
Proposition
Les similitudes directes du plan complexe sont les transformations
(avec
et
des nombres complexes). Les similitudes indirectes du plan complexe sont les transformations
(avec
et
des nombres complexes).
Définition
On appelle rapport de la similitude la valeur absolue du rapport de l'homothétie, il vaut
dans l'écriture complexe.
Géométrie du plan complexe
→
V Similitudes
→ V-1 Définitions et propriétés
V-2 Exemples
Géométrie du plan complexe
→
V Similitudes
→ V-2 Exemples
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Voici quelques exemples de similitudes et une remarque importante sur la décomposition d'une similitude.
Exemples
- Les isométries sont des similitudes de rapport .
- L'homothétie est une similitude de rapport , elle est la composée de et la symétrie centrale .
Remarque
Si
n'est pas réel,
est la composée de la rotation
avec
et
et de l'homothétie de centre
et de rapport
.
Mais cette composition n'est pas commutative.
En effet on a :
Géométrie du plan complexe
→
V Similitudes
→ V-2 Exemples
VI Etude des similitudes qui ne sont pas des isométries
Géométrie du plan complexe
→ VI Etude des similitudes qui ne sont pas des isométries
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Dans cette partie, on étudie les similitudes qui ne sont pas des isométries, c'est-à-dire leur rapport est différent de
.
VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
Géométrie du plan complexe
→ VI Etude des similitudes qui ne sont pas des isométries
VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
On va maintenant montrer qu'on peut écrire une similitude qui n'est pas une isométrie comme composée commutative d'une homothétie et d'une isométrie à point fixe.
Démonstration
Proposition
Soit
une similitude qui n'est pas une
isométrie (
dans son écriture complexe). Alors
admet un unique point fixe, noté
d'affixe
, appelé centre de la similitude.
Alors, si est le rapport de , on peut écrire où est une isométrie admettant comme point fixe. Cette écriture est appelée décomposition canonique de .
Alors, si est le rapport de , on peut écrire où est une isométrie admettant comme point fixe. Cette écriture est appelée décomposition canonique de .
Démonstration
L'existence et l'unicité du point fixe sont démontrées
ici
et
là
. Supposons que
fixe le point
d'affixe
.
Si la similitude est directe, pour commencer, alors on a et donc . Prenons comme origine ; dans ce nouveau repère, l'affixe d'un point vaut . On a donc
La similitude
est donc la composée commutative de
et d'une isométrie (le complexe
est de module
) qui fixe la nouvelle origine
, c'est-à-dire une rotation de centre
.
Si est indirecte, on fait le même calcul sans problème avec des conjugués aux bons endroits et on écrit donc comme composée de l'homothétie et d'une isométrie négative qui fixe , donc une réflexion.
Si la similitude est directe, pour commencer, alors on a et donc . Prenons comme origine ; dans ce nouveau repère, l'affixe d'un point vaut . On a donc
Si est indirecte, on fait le même calcul sans problème avec des conjugués aux bons endroits et on écrit donc comme composée de l'homothétie et d'une isométrie négative qui fixe , donc une réflexion.
Fin de la démonstration
- VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
- VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
- VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
- VI-4 Exercices
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soit
est une similitude directe
qui n'est pas une isométrie (
). Le point
est fixe par
si et seulement si
vérifie
; cette équation aux points fixes a une unique solution :
puisque
ne peut être égal à
.
Figure : Image d'un carré par une similitude directe.
Le carré est l'image de par la similitude de centre d'angle et de rapport . On peut afficher l'image de par la rotation .
Proposition
Dans le cas
, la similitude directe
admet pour centre son unique point fixe
d'affixe
et vérifie
On note
la similitude composée de
et de
. Son expression complexe est :
Figure : Image d'un carré par une similitude directe.
Le carré est l'image de par la similitude de centre d'angle et de rapport . On peut afficher l'image de par la rotation .
- VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
- VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
- VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
- VI-4 Exercices
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Considérons maintenant le cas d'une similitude indirecte
qui n'est pas une isométrie (
) et recherchons les éventuels points fixes de
.
Si est un point fixe de , alors est un point fixe de . La réciproque est fausse, il suffit de considérer une réflexion : son carré est l'identité, donc admet tout point comme point fixe.
Déterminons donc les éventuels points fixes de :
Comme on a supposé
, l'application
a un unique point fixe
d'affixe
.
Vérifions que est point fixe de .
On a bien
.
Figure : Image d'un triangle par une similitude indirecte.
Le triangle est l'image de par la similitude de centre d'axe et de rapport . On peut faire apparaître le symétrique par rapport à .
Si est un point fixe de , alors est un point fixe de . La réciproque est fausse, il suffit de considérer une réflexion : son carré est l'identité, donc admet tout point comme point fixe.
Déterminons donc les éventuels points fixes de :
Vérifions que est point fixe de .
Proposition
Dans le cas
, la similitude indirecte
admet comme centre
son unique point fixe
d'affixe
. Elle est
la composée de l'homothétie
et de la réflexion d'axe
passant par
et faisant un angle
(modulo
 ) avec l'axe des abscisses.
On note
. Posons
.
L'expression complexe de
est :
.
) avec l'axe des abscisses.
On note
. Posons
.
L'expression complexe de
est :
.
 ) avec l'axe des abscisses.
) avec l'axe des abscisses.
Figure : Image d'un triangle par une similitude indirecte.
Le triangle est l'image de par la similitude de centre d'axe et de rapport . On peut faire apparaître le symétrique par rapport à .
- VI-1 Décomposition canonique d'une similitude qui n'est pas une isométrie
- VI-2 Point fixe d'une similitude directe qui n'est pas une isométrie
- VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
- VI-4 Exercices
Géométrie du plan complexe
→
VI Etude des similitudes qui ne sont pas des isométries
→ VI-3 Point fixe d'une similitude indirecte qui n'est pas une isométrie
VI-4 Exercices
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Certains exercices admettent pour le centre ou le vecteur des expressions non simplifiées.
- Ecriture complexe d'une similitude directe
- Centre et rapport d'une similitude directe
- Type d'une similitude directe
- Similitude directe définie géométriquement dans un polygone
- Type d'une similitude et éléments caractéristiques
VII Composition des similitudes
Géométrie du plan complexe
→ VII Composition des similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
VII-2 Similitudes et angles orientés
Nous allons préciser les éléments caractéristiques de la composée de deux similitudes directes.
Géométrie du plan complexe
→ VII Composition des similitudes
VII-1 Groupe des similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-1 Groupe des similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Nous savons déjà que toute isométrie est inversible. Inversons maintenant une similitude qui n'est pas une isométrie.
VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
Nous étudions maintenant la composée de deux similitudes.- VII-1 Groupe des similitudes
- VII-2 Similitudes et angles orientés
- VII-3 Composées de similitudes directes
- VII-4 Exercices de composition
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-1 Groupe des similitudes
VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soient
un réel positif différent de
et
,
 un réel,
un point du plan,
un réel,
un point du plan,
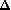 une droite passant par
.
Nous avons vu les inverses des isométries dans le document
Isométries du plan
et celui d'une homothétie
ici
. Comme la décomposition canonique est commutative, nous en déduisons :
une droite passant par
.
Nous avons vu les inverses des isométries dans le document
Isométries du plan
et celui d'une homothétie
ici
. Comme la décomposition canonique est commutative, nous en déduisons :
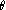 un réel,
un point du plan,
un réel,
un point du plan,
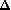 une droite passant par
.
Nous avons vu les inverses des isométries dans le document
Isométries du plan
et celui d'une homothétie
ici
. Comme la décomposition canonique est commutative, nous en déduisons :
une droite passant par
.
Nous avons vu les inverses des isométries dans le document
Isométries du plan
et celui d'une homothétie
ici
. Comme la décomposition canonique est commutative, nous en déduisons :
Proposition
- L'inverse de est
- L'inverse de est .
- VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
- VII-1-2 Composées de similitudes
- VII-1-3 Groupe des similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
VII-1-2 Composées de similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-2 Composées de similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Nous caractérisons les similitudes comme les applications du plan qui conservent les rapports de longueur.
Démonstration
De cette caractérisation des similitudes, nous déduisons que la composée de deux similitudes est une similitude. Plus précisément, comme une similitude multiplie les longueurs par son rapport, le rapport de la composée de deux similitudes est une similitude de rapport le produit des rapports.
Proposition
Les similitudes sont les applications qui conservent le rapport des longueurs.
Démonstration
Nous avons défini une similitude comme la composée d'une homothétie et d'une isométrie.
Il en résulte facilement qu'une similitude conserve le rapport des longueurs. En effet, soit
une similitude de rapport
et deux points
,
(resp.
et
) distincts alors des égalités
et
, on déduit
.
Réciproquement, soit une application du plan qui conserve le rapport des longueurs. Alors pour deux points quelconques et (resp. et ) distincts, on peut écrire . On en déduit l'égalité de rapports :
Notons
la valeur commune des rapports
. On a donc montré que
multiplie les longueurs par
; on en déduit que
est une isométrie donc
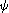 est une similitude.
est une similitude.
Réciproquement, soit une application du plan qui conserve le rapport des longueurs. Alors pour deux points quelconques et (resp. et ) distincts, on peut écrire . On en déduit l'égalité de rapports :
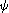 est une similitude.
est une similitude.
Fin de la démonstration
De cette caractérisation des similitudes, nous déduisons que la composée de deux similitudes est une similitude. Plus précisément, comme une similitude multiplie les longueurs par son rapport, le rapport de la composée de deux similitudes est une similitude de rapport le produit des rapports.
- VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
- VII-1-2 Composées de similitudes
- VII-1-3 Groupe des similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-2 Composées de similitudes
VII-1-3 Groupe des similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-3 Groupe des similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Pour la définition d'un groupe et des exemples, consultez le document
Isométries du plan
. Des deux paragraphes précédents on déduit :
Proposition
L'ensemble des similitudes du plan complexe est un groupe pour la loi de composition.
- VII-1-1 Inverse d'une similitude qui n'est pas une isométrie
- VII-1-2 Composées de similitudes
- VII-1-3 Groupe des similitudes
Géométrie du plan complexe
→
VII Composition des similitudes
→
VII-1 Groupe des similitudes
→ VII-1-3 Groupe des similitudes
VII-2 Similitudes et angles orientés
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-2 Similitudes et angles orientés
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Une homothétie conserve les angles orientés.
Démonstration
Soit un réel
différent de
et
et
un point du plan. On considère trois points distincts
,
et
et leurs images
,
et
par
. La relation de Chasles et la définition de
permettent d'écrire :
On en déduit que l'angle orienté
est égal à l'angle
, on peut donc affirmer qu'une homothétie conserve les angles orientés.
Fin de la démonstration
On en déduit la proposition suivante.
Proposition
- Une similitude directe conserve les angles orientés.
- Une similitude indirecte conserve les angles géométriques et transforme un angle orienté en son opposé.
Proposition
- La composée de deux similitudes directes (ou de deux similitudes indirectes) est une similitude directe.
- La composée d'une similitude directe et d'une similitude indirecte est une similitude indirecte.
Corollaire
L'ensemble des similitudes directes du plan complexe est un groupe pour la loi de composition.
- VII-1 Groupe des similitudes
- VII-2 Similitudes et angles orientés
- VII-3 Composées de similitudes directes
- VII-4 Exercices de composition
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-2 Similitudes et angles orientés
VII-3 Composées de similitudes directes
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-3 Composées de similitudes directes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soient deux réels et différents de et , deux angles et et deux points et .
La composée a pour écriture complexe :
Nous pouvons maintenant énoncer la proposition suivante :
Proposition
Soient deux réels
et
différents de
et
, deux angles
et
et deux points
et
.
- Si n'est pas nul alors la composée est la similitude dont on aura à déterminer le centre .
- Si n'est pas nul et que vaille , la similitude composée est une rotation d'angle .
- Si est nul et différent de , la composée est une homothétie de rapport dont on aura à déterminer le centre.
- Si est nul et égal à , la composée est une translation.
Corollaire
L'ensemble des homothéties et des translations est un groupe pour la loi de composition.
Démonstration
On savait déjà que les translations forment un groupe ; la proposition précédente permet d'affirmer que la composée d'une translation et d'une homothétie est une homothétie et que la composée de deux homothéties est une homothétie ou une translation.
Fin de la démonstration
- VII-1 Groupe des similitudes
- VII-2 Similitudes et angles orientés
- VII-3 Composées de similitudes directes
- VII-4 Exercices de composition
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-3 Composées de similitudes directes
VII-4 Exercices de composition
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-4 Exercices de composition
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Voici quelques exercices pour s'entraîner à composer des similitudes en écriture complexes.
- Composée translation et symétrie centrale
- Composée d'homothétie et translation
- Composée d'une translation et d'une rotation
- Composée de deux rotations
- VII-1 Groupe des similitudes
- VII-2 Similitudes et angles orientés
- VII-3 Composées de similitudes directes
- VII-4 Exercices de composition
Géométrie du plan complexe
→
VII Composition des similitudes
→ VII-4 Exercices de composition
VIII Propriétés des similitudes
Géométrie du plan complexe
→ VIII Propriétés des similitudes
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Géométrie du plan complexe
→ VIII Propriétés des similitudes
VIII-1 Figures semblables
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-1 Figures semblables
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Les isométries conservent forme et taille d'une figure. Les similitudes qui ne sont pas des isométries conservent la forme des figures mais seul le rapport des longueurs est conservé.
Figures semblables
Ensemble de figures semblables
Définition
On dit que deux figures sont semblables si l'une est la transformée de l'autre par une similitude.
Exercices
Figures semblables
Ensemble de figures semblables
- VIII-1 Figures semblables
- VIII-2 Similitude définie par l'image de deux points donnés
- VIII-3 Image d'une droite ou d'un cercle
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-1 Figures semblables
VIII-2 Similitude définie par l'image de deux points donnés
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-2 Similitude définie par l'image de deux points donnés
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Proposition
Soient
et
(resp.
et
) deux
points distincts. Il existe une unique similitude directe (resp. indirecte)
telle que l'on ait
Démonstration
Notons
,
,
et
les affixes respectives de
,
,
et
'.
Recherche de la similitude directe. On sait qu'une similitude directe a pour expression complexe . On cherche donc deux nombres complexes et tels que
Pour trouver
, on retranche la deuxième équation à la première. Pour trouver
, on multiplie la première (respectivement seconde) équation par
(resp.
) et on retranche la deuxième équation à la première. Comme
et
sont distincts (
), on obtient :
Comme
et
sont distincts (
), le complexe
n'est pas nul.
L'expression de signifie que le rapport de la similitude est et que son angle est .
Recherche de la similitude indirecte. On sait qu'une similitude indirecte a pour expression complexe . On cherche donc deux nombres complexes et tels que
La seule solution est alors
A nouveau, le rapport est
.
Recherche de la similitude directe. On sait qu'une similitude directe a pour expression complexe . On cherche donc deux nombres complexes et tels que
L'expression de signifie que le rapport de la similitude est et que son angle est .
Recherche de la similitude indirecte. On sait qu'une similitude indirecte a pour expression complexe . On cherche donc deux nombres complexes et tels que
Fin de la démonstration
Exercice
Ecriture complexe d'une similitude donnée par l'image de deux points
- VIII-1 Figures semblables
- VIII-2 Similitude définie par l'image de deux points donnés
- VIII-3 Image d'une droite ou d'un cercle
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-2 Similitude définie par l'image de deux points donnés
VIII-3 Image d'une droite ou d'un cercle
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-3 Image d'une droite ou d'un cercle
- I Géométrie du plan complexe
- II Ecriture complexe d'une transformation
- III Isométries du plan complexe
- IV Homothétie
- V Similitudes
- VI Etude des similitudes qui ne sont pas des isométries
- VII Composition des similitudes
- VIII Propriétés des similitudes
Soient
et
deux points distincts d'affixes respectives
et
,
et
deux réels strictement positifs.
En utilisant les propriétés des homothéties, des isométries et de la décomposition canonique, on montre que l'image de par une similitude est la droite .
L'image du cercle de centre et de rayon par une similitude de rapport est le cercle en effet on a, pour tout point du plan, d'affixe :
En utilisant les propriétés des homothéties, des isométries et de la décomposition canonique, on montre que l'image de par une similitude est la droite .
L'image du cercle de centre et de rayon par une similitude de rapport est le cercle en effet on a, pour tout point du plan, d'affixe :
- VIII-1 Figures semblables
- VIII-2 Similitude définie par l'image de deux points donnés
- VIII-3 Image d'une droite ou d'un cercle
Géométrie du plan complexe
→
VIII Propriétés des similitudes
→ VIII-3 Image d'une droite ou d'un cercle